红黑树并没有我们想象的那么难 上、下两篇已经完成, 希望能帮助到大家.
-
红黑树并没有我们想象的那么难(上): http://daoluan.github.io/blog/rbtree-is-not-difficult/
-
红黑树并没有我们想象的那么难(下): http://daoluan.github.io/blog/rbtree-is-not-difficult-2/
SGI STL map 实现概述
根据上一节的红黑树分析, 结合 sgi stl map 的实现, 看看红黑树的源码是如何实现的. 以下主要以代码的注释为主.
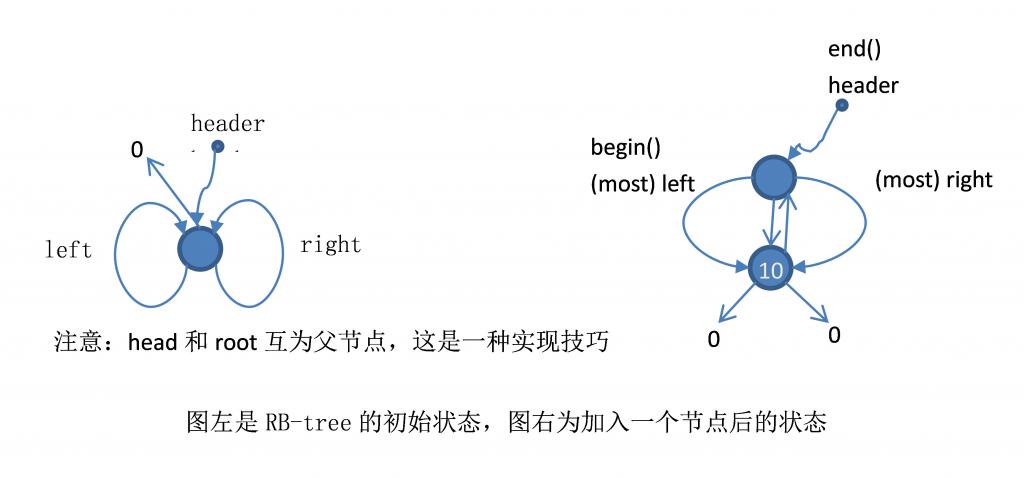
sgi stl map 底层实现是 _Rb_tree类, 为了方便管理, _Rb_tree 内置了 _M_header, 用于记录红黑树中的根节点, 最小节点和最大节点. 在插入删除中都会对其进行维护. 找到一副美艳的图片:
我只会展开插入和删除的代码. _Rb_tree 有 insert_unique() 和 insert_equal() 两种, 前者不允许有重复值, 后者可以. insert_unique() 判断是否有重复值的方法利用了二叉搜索树的性质. 细节请参看下面的代码.
为什么选择红黑树作为底层实现
红黑树是一种类平衡树, 但它不是高度的平衡树, 但平衡的效果已经很好了. 补充说明另一种 AVL 树, 我之前的博文: 《编程珠玑,字字珠玑》读书笔记完结篇——AVL树
用过 STL map 么, 你用过 linux 么(这个说大了), 他们都有红黑树的应用. 当你对搜索的效率要求较高,并且数据经常改动的情景,你可以用红黑树, 也就是 map.
至于, 为什么不用 AVL 树作为底层实现, 那是因为 AVL 树是高度平衡的树, 而每一次对树的修改, 都要 rebalance, 这里的开销会比红黑树大. 红黑树插入只要两次旋转, 删除至多三次旋转. 但不可否认的是, AVL 树搜索的效率是非常稳定的. 选取红黑树, 我认为是一种折中的方案.
红黑树源代码剖析
// sgi stl _Rb_tree 插入算法 insert_equal() 实现.
// 策略概述: insert_equal() 在红黑树找到自己的位置,
// 然后交由 _M_insert() 来处理接下来的工作.
// _M_insert() 会将节点插入红黑树中, 接着调整红黑树,
// 维持性质.
template <class _Key, class _Value, class _KeyOfValue,
class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
::insert_equal(const _Value& __v)
{
// 在红黑树中有头结点和根节点的概念, 头结点位于根节点之上,
// 头结点只为管理而存在, 根节点是真正存储数据的地方. 头结点和根节点互为父节点,
// 是一种实现的技巧.
_Link_type __y = _M_header; // 指向头结点
_Link_type __x = _M_root(); // _M_header->_M_parent, 即指向根节点
// 寻找插入的位置
while (__x != 0) {
__y = __x;
// 小于当前节点要走左边, 大于等于当前节点走右边
__x = _M_key_compare(_KeyOfValue()(__v), _S_key(__x)) ?
_S_left(__x) : _S_right(__x);
}
// __x 为需要插入的节点的位置, __y 为其父节点
return _M_insert(__x, __y, __v);
}
// sgi stl _Rb_tree 插入算法 insert_unique() 实现.
// 策略概述: insert_unique() 同样也在红黑树中找到自己的位置; 我们知道,
// 如果小于等于当前节点会往右走, 所以遇到一个相同键值的节点后, 会往右走一步,
// 接下来一直往左走, 所以下面的实现会对往左走的情况做特殊的处理.
template <class _Key, class _Value, class _KeyOfValue,
class _Compare, class _Alloc>
pair<typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator,
bool>
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
::insert_unique(const _Value& __v)
{
_Link_type __y = _M_header; // 指向头结点
_Link_type __x = _M_root(); // 指向根节点, 可能为空
bool __comp = true;
// 寻找插入的位置
while (__x != 0) {
__y = __x;
__comp = _M_key_compare(_KeyOfValue()(__v), _S_key(__x));
// 小于当前节点要走左边, 大于等于当前节点走右边
__x = __comp ? _S_left(__x) : _S_right(__x);
}
iterator __j = iterator(__y); // 在 __y 上建立迭代器
// 我认为下面判断树中是否有存在键值的情况有点绕,
// 它充分利用了二叉搜索树的性质, 如此做很 hack, 但不易理解.
// 要特别注意往左边插入的情况.
// HACKS:
// 下面的 if 语句是比 __x 小走左边的情况: 会发现, 如果插入一个已存在的键的话,
// __y 最终会定位到已存在键的右子树的最左子树.
// 譬如, 红黑树中已经存在一个键为 100 的节点, 其右孩子节点为 101,
// 此时如果再插入键为 100 的节点, 因为 100<=100, 所以会往右走到达 101 节点,
// 有 100<101, 继而往左走, 会一直往左走.大家稍微画一个例子就能理解.
if (__comp)
// 特殊情况, 如果 __j 指向了最左孩子, 那么肯定要插入新节点.
if (__j == begin())
return pair<iterator,bool>(_M_insert(__x, __y, __v), true);
// 其他情况, 这个时候也是往左边插入, 如果存在重复的键值,
// 那么 --__j 能定位到此重复的键的节点.
else
--__j;
// HACKS: 这里比较的是 __j 和 __v, 如果存在键值, 那么 __j == __v,
// 会跳过 if 语句. 否则执行插入. 也就是说如果存在重复的键, 那么 __j
// 的值肯定是等于 __v
if (_M_key_compare(_S_key(__j._M_node), _KeyOfValue()(__v)))
return pair<iterator,bool>(_M_insert(__x, __y, __v), true);
// 此时 __y.value = __v, 不允许插入, 返回键值所在位置
return pair<iterator,bool>(__j, false);
}
// _M_insert() 是真正执行插入的地方.
// 策略概述: 插入策略已经在上篇中详述, 可以根据上篇文章的描述,
// 和下面代码的注释, 加深对红黑树插入算法里理解
template <class _Key, class _Value, class _KeyOfValue,
class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
::_M_insert(_Base_ptr __x_, _Base_ptr __y_, const _Value& __v)
{
_Link_type __x = (_Link_type) __x_; // 新节点插入的位置.
// 关于 __x 的疑问:
// 1. 它被放到下面的, 第一个 if 语句中, 我觉得是没有必要的,
// 因为从调用 _M_insert() 的函数来看, __x 总是为空.
// 2. 既然 __x 是新节点插入的位置, 那么为什么不直接在 __x 上创建节点,
// 还要在下面通过比较来决定新节点是左孩子还是右孩子;
// 不如直接用指针的指针或者指针的引用来完成, 省去了下面的判断.
_Link_type __y = (_Link_type) __y_; // 新节点的父节点
_Link_type __z; // 新节点的位置
if (__y == _M_header || __x != 0 ||
_M_key_compare(_KeyOfValue()(__v), _S_key(__y))) {
// 新节点应该为左孩子
__z = _M_create_node(__v);
_S_left(__y) = __z; // also makes _M_leftmost() = __z
// when __y == _M_header
if (__y == _M_header) {
_M_root() = __z;
_M_rightmost() = __z;
}
else if (__y == _M_leftmost())
_M_leftmost() = __z; // maintain _M_leftmost() pointing to min node
}
// 新节点应该为右孩子
else {
__z = _M_create_node(__v);
_S_right(__y) = __z;
if (__y == _M_rightmost())
_M_rightmost() = __z; // maintain _M_rightmost() pointing to max node
}
_S_parent(__z) = __y;
_S_left(__z) = 0;
_S_right(__z) = 0;
// 重新调整
_Rb_tree_rebalance(__z, _M_header->_M_parent);
// 更新红黑树节点数
++_M_node_count;
// 返回迭代器类型
return iterator(__z);
}
// 插入新节点后, 可能会破坏红黑树性质, _Rb_tree_rebalance() 负责维持性质.
// 其中:
// __x 新插入的节点
// __root 根节点
// 策略概述: 红黑树插入重新调整的策略已经在上篇中讲述,
// 可以结合上篇文章和这里的代码注释,
// 理解红黑树的插入算法.
inline void
_Rb_tree_rebalance(_Rb_tree_node_base* __x, _Rb_tree_node_base*& __root)
{
// 将新插入的节点染成红色
__x->_M_color = _S_rb_tree_red;
while (__x != __root && __x->_M_parent->_M_color == _S_rb_tree_red) {
// __x 的父节点也是红色的情况. 提示: 如果是黑色节点, 不会破坏红黑树性质.
if (__x->_M_parent == __x->_M_parent->_M_parent->_M_left) {
// 叔父节点
_Rb_tree_node_base* __y = __x->_M_parent->_M_parent->_M_right;
if (__y && __y->_M_color == _S_rb_tree_red) {
// 第 1 种情况, N,P,U 都红(G 肯定黑).
// 策略: G->红, N,P->黑. 此时, G 红, 如果 G 的父亲也是红, 性质又被破坏了,
// HACK: 可以将 GPUN 看成一个新的红色 N 节点, 如此递归调整下去;
// 特俗的, 如果碰巧将根节点染成了红色, 可以在算法的最后强制 root->红.
__x->_M_parent->_M_color = _S_rb_tree_black;
__y->_M_color = _S_rb_tree_black;
__x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;
__x = __x->_M_parent->_M_parent;
}
else {
if (__x == __x->_M_parent->_M_right) {
// 第 2 种情况, P 为红, N 为 P 右孩子, U 为黑或缺少.
// 策略: 旋转变换, 从而进入下一种情况:
__x = __x->_M_parent;
_Rb_tree_rotate_left(__x, __root);
}
// 第 3 种情况, 可能由第二种变化而来, 但不是一定: P 为红, N 为红.
// 策略: 旋转, 交换 P,G 颜色, 调整后, 因为 P 为黑色, 所以不怕
// P 的父节点是红色的情况. over
__x->_M_parent->_M_color = _S_rb_tree_black;
__x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;
_Rb_tree_rotate_right(__x->_M_parent->_M_parent, __root);
}
}
else { // 下面的代码是镜像得出的, 脑补吧.
_Rb_tree_node_base* __y = __x->_M_parent->_M_parent->_M_left;
if (__y && __y->_M_color == _S_rb_tree_red) {
__x->_M_parent->_M_color = _S_rb_tree_black;
__y->_M_color = _S_rb_tree_black;
__x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;
__x = __x->_M_parent->_M_parent;
}
else {
if (__x == __x->_M_parent->_M_left) {
__x = __x->_M_parent;
_Rb_tree_rotate_right(__x, __root);
}
__x->_M_parent->_M_color = _S_rb_tree_black;
__x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;
_Rb_tree_rotate_left(__x->_M_parent->_M_parent, __root);
}
}
}
__root->_M_color = _S_rb_tree_black;
}
// 删除算法, 直接调用底层的删除实现 _Rb_tree_rebalance_for_erase().
template <class _Key, class _Value, class _KeyOfValue,
class _Compare, class _Alloc>
inline void _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
::erase(iterator __position)
{
_Link_type __y =
(_Link_type) _Rb_tree_rebalance_for_erase(__position._M_node,
_M_header->_M_parent,
_M_header->_M_left,
_M_header->_M_right);
destroy_node(__y);
--_M_node_count;
}
// 删除节点底层实现, 删除可能会破坏红黑树性质,
// _Rb_tree_rebalance()
// 负责维持性质. 其中:
// __z 需要删除的节点
// __root 根节点
// __leftmost 红黑树内部数据, 即最左子树
// __rightmost 红黑树内部数据, 即最右子树
// 策略概述: _Rb_tree_rebalance_for_erase() 会根据
// 删除节点的位置在红黑树中找到顶替删除节点的节点,
// 即无非是删除节点左子树的最大节点或右子树中的最小节点,
// 此处用的是有一种策略. 接着, 会调整红黑树以维持性质.
// 调整的算法已经在上篇文章中详述, 可以根据上篇文章的描述
// 和此篇的代码注释, 加深对红黑树删除算法的理解.
inline _Rb_tree_node_base*
_Rb_tree_rebalance_for_erase(_Rb_tree_node_base* __z,
_Rb_tree_node_base*& __root,
_Rb_tree_node_base*& __leftmost,
_Rb_tree_node_base*& __rightmost)
{
// __z 是要删除的节点
// __y 最终会指向要删除的节点
_Rb_tree_node_base* __y = __z;
// N 节点
_Rb_tree_node_base* __x = 0;
// 记录 N 节点的父节点
_Rb_tree_node_base* __x_parent = 0;
// 只有一个孩子或者没有孩子的情况
if (__y->_M_left == 0) // __z has at most one non-null child. y == z.
__x = __y->_M_right; // __x might be null.
else
if (__y->_M_right == 0) // __z has exactly one non-null child. y == z.
__x = __y->_M_left; // __x is not null.
// 有两个非空孩子
else { // __z has two non-null children. Set __y to
__y = __y->_M_right; // __z's successor. __x might be null.
// __y 取右孩子中的最小节点, __x 记录他的右孩子(可能存在右孩子)
while (__y->_M_left != 0)
__y = __y->_M_left;
__x = __y->_M_right;
}
// __y != __z 说明有两个非空孩子的情况,
// 此时的删除策略就和文中提到的普通二叉搜索树删除策略一样:
// __y 记录了 __z 右子树中最小的节点
// __x 记录了 __y 的右孩子
// 用 __y 顶替 __z 的位置, __x 顶替 __y 的位置, 最后用 __y 指向 __z,
// 从而 __y 指向了要删除的节点
if (__y != __z) { // relink y in place of z. y is z's successor
// 将 __z 的记录转移至 __y 节点
__z->_M_left->_M_parent = __y;
__y->_M_left = __z->_M_left;
// 如果 __y 不是 __z 的右孩子, __z->_M_right 有左孩子
if (__y != __z->_M_right) {
__x_parent = __y->_M_parent;
// 如果 __y 有右孩子 __x, 必须有那个 __x 替换 __y 的位置
if (__x)
// 替换 __y 的位置
__x->_M_parent = __y->_M_parent;
__y->_M_parent->_M_left = __x; // __y must be a child of _M_left
__y->_M_right = __z->_M_right;
__z->_M_right->_M_parent = __y;
}
// __y == __z->_M_right
else
__x_parent = __y;
// 如果 __z 是根节点
if (__root == __z)
__root = __y;
// __z 是左孩子
else if (__z->_M_parent->_M_left == __z)
__z->_M_parent->_M_left = __y;
// __z 是右孩子
else
__z->_M_parent->_M_right = __y;
__y->_M_parent = __z->_M_parent;
// 交换需要删除节点 __z 和 替换节点 __y 的颜色
__STD::swap(__y->_M_color, __z->_M_color);
__y = __z;
// __y now points to node to be actually deleted
}
// __y == __z 说明至多一个孩子
else { // __y == __z
__x_parent = __y->_M_parent;
if (__x) __x->_M_parent = __y->_M_parent;
// 将 __z 的父亲指向 __x
if (__root == __z)
__root = __x;
else
if (__z->_M_parent->_M_left == __z)
__z->_M_parent->_M_left = __x;
else
__z->_M_parent->_M_right = __x;
// __leftmost 和 __rightmost 是红黑树的内部数据, 因为 __z 可能是
// __leftmost 或者 __rightmost, 因此需要更新.
if (__leftmost == __z)
if (__z->_M_right == 0) // __z->_M_left must be null also
// __z 左右孩子都为空, 没有孩子
__leftmost = __z->_M_parent;
// makes __leftmost == _M_header if __z == __root
else
__leftmost = _Rb_tree_node_base::_S_minimum(__x);
if (__rightmost == __z)
if (__z->_M_left == 0) // __z->_M_right must be null also
__rightmost = __z->_M_parent;
// makes __rightmost == _M_header if __z == __root
else // __x == __z->_M_left
__rightmost = _Rb_tree_node_base::_S_maximum(__x);
// __y 同样已经指向要删除的节点
}
// __y 指向要删除的节点
// __x 即为 N 节点
// __x_parent 指向 __x 的父亲, 即 N 节点的父亲
if (__y->_M_color != _S_rb_tree_red) {
// __y 的颜色为黑色的时候, 会破坏红黑树性质
while (__x != __root && (__x == 0 || __x->_M_color == _S_rb_tree_black))
// __x 不为红色, 即为空或者为黑. 提示: 如果 __x 是红色, 直接将 __x 替换成黑色
if (__x == __x_parent->_M_left) { // 如果 __x 是左孩子
_Rb_tree_node_base* __w = __x_parent->_M_right; // 兄弟节点
if (__w->_M_color == _S_rb_tree_red) {
//第 2 情况, S 红, 根据红黑树性质P,SL,SR 一定黑.
// 策略: 旋转, 交换 P,S 颜色.
__w->_M_color = _S_rb_tree_black;
__x_parent->_M_color = _S_rb_tree_red; // 交换颜色
_Rb_tree_rotate_left(__x_parent, __root); // 旋转
__w = __x_parent->_M_right; // 调整关系
}
if ((__w->_M_left == 0 ||
__w->_M_left->_M_color == _S_rb_tree_black) &&
(__w->_M_right == 0 ||
__w->_M_right->_M_color == _S_rb_tree_black)) {
// 提示: 这是 第 1 情况和第 2.1 情况的合并, 因为处理的过程是一样的.
// 但他们的情况还是要分门别类的. 已经在文章中详细支出,
// 似乎大多数的博文中没有提到这一点.
// 第 1 情况, N,P,S,SR,SL 都黑.
// 策略: S->红. 通过 PN,PS 的黑色节点数量相同了, 但会比其他路径多一个,
// 解决的方法是在 P 上从情况 0 开始继续调整.
// 为什么要这样呢? HACKS: 因为既然 PN,PS
// 路径上的黑节点数量相同而且比其他路径会少一个黑节点,
// 那何不将其整体看成了一个 N 节点! 这是递归原理.
// 第 2.1 情况, S,SL,SR 都黑.
// 策略: P->黑. S->红, 因为通过 N 的路径多了一个黑节点,
// 通过 S 的黑节点个数不变, 所以维持了性质 5. over
// 可能大家会有疑问, 不对啊, 2.1 的情况,
// 策略是交换父节点和兄弟节点的颜色, 此时怎么没有对父节点的颜色赋值呢?
// HACKS: 这就是合并情况的好处, 因为就算此时父节点是红色,
// 而且也将兄弟节点颜色改为红色, 你也可以将 PS,PN 看成一个红色的 N 节点,
// 这样在下一个循环当中, 这个 N 节点也会变成黑色. 因为此函数最后有一句话:
// if (__x) __x->_M_color = _S_rb_tree_black;
// 合并情况, 节省代码量
// 当然是可以分开写的
// 兄弟节点染成红色
__w->_M_color = _S_rb_tree_red;
// 调整关系
__x = __x_parent;
__x_parent = __x_parent->_M_parent;
} else {
if (__w->_M_right == 0 ||
__w->_M_right->_M_color == _S_rb_tree_black) {
// 第 2.2.1 情况, S,SR 黑, SL 红.
// 策略: 旋转, 变换 SL,S 颜色.
if (__w->_M_left) __w->_M_left->_M_color = _S_rb_tree_black;
__w->_M_color = _S_rb_tree_red;
_Rb_tree_rotate_right(__w, __root);
// 调整关系
__w = __x_parent->_M_right;
}
// 第 2.2.2 情况, S 黑, SR 红.
// 策略: 旋转, 交换 S,P 颜色, SR->黑色, 重新获得平衡.
__w->_M_color = __x_parent->_M_color;
__x_parent->_M_color = _S_rb_tree_black;
if (__w->_M_right) __w->_M_right->_M_color = _S_rb_tree_black;
_Rb_tree_rotate_left(__x_parent, __root);
break;
} // 下面的代码是镜像得出的, 脑补吧.
} else { // same as above, with _M_right <-> _M_left.
_Rb_tree_node_base* __w = __x_parent->_M_left;
if (__w->_M_color == _S_rb_tree_red) {
__w->_M_color = _S_rb_tree_black;
__x_parent->_M_color = _S_rb_tree_red;
_Rb_tree_rotate_right(__x_parent, __root);
__w = __x_parent->_M_left;
}
if ((__w->_M_right == 0 ||
__w->_M_right->_M_color == _S_rb_tree_black) &&
(__w->_M_left == 0 ||
__w->_M_left->_M_color == _S_rb_tree_black)) {
__w->_M_color = _S_rb_tree_red;
__x = __x_parent;
__x_parent = __x_parent->_M_parent;
} else {
if (__w->_M_left == 0 ||
__w->_M_left->_M_color == _S_rb_tree_black) {
if (__w->_M_right) __w->_M_right->_M_color = _S_rb_tree_black;
__w->_M_color = _S_rb_tree_red;
_Rb_tree_rotate_left(__w, __root);
__w = __x_parent->_M_left;
}
__w->_M_color = __x_parent->_M_color;
__x_parent->_M_color = _S_rb_tree_black;
if (__w->_M_left) __w->_M_left->_M_color = _S_rb_tree_black;
_Rb_tree_rotate_right(__x_parent, __root);
break;
}
}
if (__x) __x->_M_color = _S_rb_tree_black;
}
return __y;
}
Dylan 2013-9-29
28 September 2013 会持续更新