如:-5,7,1,9,-12,15 变成 -5,-12,7,1,9,15。如何解?
题目要求: 空间复杂度O(1),时间复杂度O(N),排序稳定。
空间上只能利用循环变量,标记变量等;时间上可以说是过一遍数组就完事了。
分治
用分治可以解决问题:首先把规模为 N 的问题划分成两个规模近似为 N/2 的子问题,两个子问题得到解决后进行合并得到整个问题的答案。对于本篇的问题,主要考虑合并该怎么解决,也就是假设:
将数组 arr 分成 arr1 和 arr2。设 arr1 为 [—-++++],arr2 为 [——+++],如何得到 arr 为 [———-+++++++]。
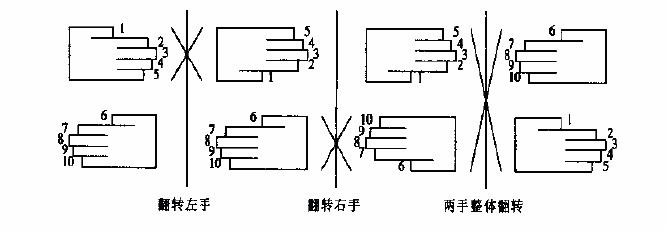
显然,只要将 arr1 的所有正数和 arr2 的所有负数交换就好了,为了不打乱原有正数/负数的次序,而且不借用任何其他的空间,考虑用《编程珠玑》中提到的 Doug Mcllroy 提出的翻手例子:
翻手代码在时间和空间上都很高效,而且代码非常的简短,很难出错。
于是方法是:将 arr1 中的正数 reverse 一次,arr2 中的负数 reverse 一次,紧接着 arr1 中的正数和 arr2 中的 负数结合起来 reverse 一次,由此完成 arr1 和 arr2 的合并。子问题就解决了。
void merge(int *arr,int left,int middle,int right)
{
/*全负数*/ /*全正数*/
if(!(arr[middle]>0 && arr[middle+1]<0))
return;
// 找到 +++++ ----- 区域
int pos1 = left,pos2 = middle + 1;
for(int i=left; i<=middle; i++)
if(arr[i] > 0) {pos1 = i;break;}
for(i=middle+1; i<=right; i++)
if(arr[i] > 0) {pos2 = i-1;break;}
// 翻手定律,你懂得
reverse(arr+pos1,middle - pos1+1);
reverse(arr+middle+1,pos2 - middle);
reverse(arr+pos1,pos2 - pos1 + 1);
}
迭代
另外,通过翻手方法同样可以迭代解决这个问题,也就是把 arr 走一遍就可以解决。同样,具体举例:
[……-+++–+-……]
-
刚开始扫描的时候如果一直是负数,那么不用作任何的动作
-
关键是遇上 [+++–] 的时候,需要作翻手处理,从而交换 [+++] 和 [–] 得到:[……—++++-……]
-
继续扫描得到 [+],[……—++++-……],不用处理
-
继续扫描得到 [-],[……—++++-……],需要对 [++++-] 作翻手处理,从而交换 [++++] 和 [-] 得到:[……—-++++……](此步骤和步骤 2 情况相同)
void myfunc(int *arr,int left,int right)
{
if(right <= left)
return;
bool f = false; // flag = true 表示需要进行翻转
int posbeg = -1, // 正数开始
posend, // 正数结束
negbeg, // 负数开始
negend, // 负数结束
negcount = 0; // 负数统计
for(int i = 0; i<=right; i++)
{
if(arr[i]>0)
{
if(posbeg < 0)
posend = posbeg = i;
posend = i;
for(int j=i+1; j<=right; j++)
if(arr[j]>0)posend++;
else break;
f = true;
i = posend + 1;
}
if(arr[i] < 0 && i <= right)
{
if(!f){negcount++;continue;}
negend = negbeg = i;
for(int j=i+1; j<=right; j++)
if(arr[j]<0)negend++,negcount++;
else break;
i = negend;
reverse(arr+posbeg,posend-posbeg+1);
reverse(arr+negbeg,negend-negbeg+1);
reverse(arr+posbeg,negend-posbeg+1);
f = false;print(arr,14);
posend = negend;
posbeg = negcount + 1;
}
}// while
}
算法复杂度
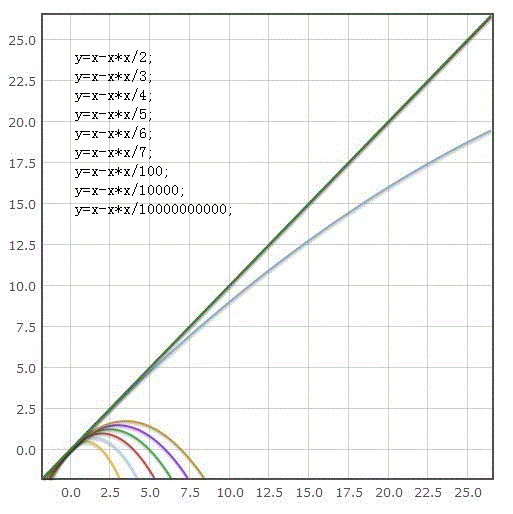
在空间上符合题目条件,但在时间上有待讨论,时间上的消耗主要在 for 循环里面的 reverse 操作。假设 arr 数组当中有 m 个正数和 n-m 的负数,在最坏的情况下,复杂度是 O(m(n-m)),平摊给 for 循环的 n 次操作,那么结果是 O(m-m^2/n))。因此,此算法不稳定。
我们来看看根据 n 和 m 的不同模拟的函数图像,将函数写成 y = x-x^2/k:
由此,这种算法确实很不稳定。一开始以为平摊法可以解决复杂度分析问题,可以达到 O(N) 的效果,但无果而终。在 CSDN 上有这题的讨论:腾讯面试题:把负数移动到正数之前,不能改变正负数原先的次序 和 微博的一个编程题 。如果你有什么好的想法,不忘给我和网友们分享一下 :),据说「之前百度就出过这道题,讨论了1000楼都没有一个正确答案」。
Dylan 2013-05-03
03 May 2013 会持续更新