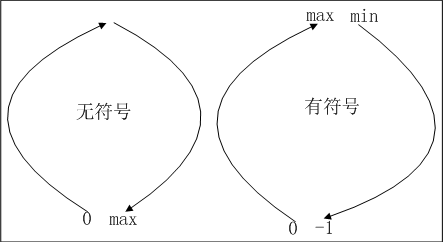
二进制数据的表示方法有原码,反码,补码。
原码即一个数据其本身的表示方式,未经过任何修改的表示方法。如 [0001 1011](27), [1001 1011](-101)
反码在形式上是原码按位取反的结果。正数的原码是其原码本身,负数的反码可由其原码最高符号位不变,其余按位取反得到。发现,反码可以表示有符号有符号整数,从 -127 ~ +127 但会出现 [0000 0000] (+0)与 [1111 1111] (−0)。补码可以填补反码的不足。有趣的是,通过反码能只通过加法来实现无符号的加减法运算。对于 4 位二进制数,x+~x+1=2^4,很明显 [0011] + [1100] + 1 = [1 0000] ,这个结论很重要。
加法就不用解释了,即是模 2^4 加法,但减法是如何变换,能通过加法实现。比如,无符号整数减法 6-11 。
0———————><——15
「4-7」就是一个蚂蚁在坐标 4 往负方向走 7 步,但是会溢出,所以返回坐标的尾端 15 继续往负方向行走,这个过程和这只蚂蚁在坐标 4 往正方向走 (16-7) 步是一样的,而 (16-7)恰好等于 (~7+1)。所以 4-7=4+~7+1=14 。所以,一个加法器可以实现加减法,即把蚂蚁的负向行走(减法)转换成正向行走(加法)。会发现,这就是补码加法。
补码。正数和 0 的补码是其本身,负数的补码则最高符号位不变,其余按位取反加 1 ,如 [0001 1011] 补码为其本身, [1001 1011] 补码为 [1110 0100] 。有趣的是,补码表示中,在w位的二进制表示中,最高的有效位被解释为负权,权重相应是负的,为 -2^( w-1 ) 。如
-
[0101 0001] = -02^7 + 12^6 + 02^5 + 12^4 + 02^3 + 02^2 + 02^1 + 12^0 = -0 + 64 + 0 + 16 + 0 + 0 + 0 + 1 = 81
-
[1101 0001] = -12^7 + 12^6 + 02^5 + 12^4 + 02^3 + 02^2 + 02^1 + 12^0 = -128 + 64 + 0 + 16 + 0 + 0 + 0 + 1 = 47
上面所说,补码规避了反码的不足:有两个 0 表示。在补码中 0 只有一种表示即 [0000 0000] , 而 [1000 0000] 也因为负权的原因只能表示最小的负数 -128 , [0111 1111] 即最大的正数 127 ,补码所能表示的范围是 -128 ~ 127 。
以 4 位二进制运算 4-7 为例,特地给出有负数的情况,正数来说,有符号和无符号预案明显是一样的。而4 位二进制有符号整数 -7 即为 4 位二进制无符号整数的 9 。有如下
-
无符号运算:4-7=4+(-7)=[0100]+~[0111]+1=[1101]=13(用上面的反码方法)
-
有符号运算:4-7=4+(-7)=[0100]+[1001]=[1101]=-3(用补码加法)
发现两者运算过程一样,结果实质上是相同的,只是机器对有符号和无符号的解释不同,因此大多数计算机使用相同的机器指令来执行无符号或者有符号的加法(减法可以代换为加法执行)。
-7 和 9是同余的,更多关于同余的概念:同余式 。
-
∵ 4≡4(mod 16)
-
又 ∵ -7≡9(mod 16)
-
根据同余式性质,得到:-7+4≡9+4(mod 16)
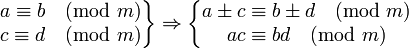 同余式性质 保持加法、减法和乘法
同余式性质 保持加法、减法和乘法
既然,对于模 16 ,4-7 和 4+9 的结果相同,CPU何不只设计只具备后者(加法)的部件?
同理,对与其他情况:
-1≡15(mod 16)
-2≡14(mod 16)
-3≡13(mod 16)
…
又一个例子:
-
无符号运算:1-5=[0001]+[1011]=[1100]=12 (为了直观,省略了上面的反码转换)又一个例子举例:
-
有符号运算:1-5=[0001]+[1011]=[1100]=-4 (红色部分是加法器的实际操作)
回到蚂蚁的例子,有符号中的负向走 5 步的 -5 ,可转变是正向走 11 步的 11,减法即被消除。上计算机组成原理课程的时候,我们经常背诵,减去一个数,就等于加上这个数的补码。补码的出现整合了无符号和有符号加减运算过程,无论机器对二进制数的解释如何,加法器所做的工作相同。当然有符号或者无符号运算都会出现正溢负溢的情况,这时需要模 2^w 操作(w:二进制位数)。
Dylan 2013-4-11
11 April 2013 会持续更新