• 写在最前面的
• 广度优先搜索
• 深度优先搜索
• 总结

写在最前面的

这篇文章并没有非常详细的算法证明过程。导论里面有非常详细的证明过程。本文只阐述“广度优先和深度优先搜索的思路以及一些简单应用”。

两种图的遍历算法在其他图的算法当中都有应用，并且是基本的图论算法。

广度优先搜索

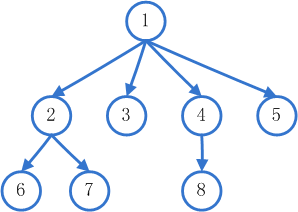
广度优先搜索（BFS），可以被形象的描述为“浅尝辄止”，具体一点就是每个顶点只访问它的邻接节点（如果它的邻接节点没有被访问）并且记录这个邻接节点，当访问完它的邻接节点之后就结束这个顶点的访问。

广度优先用到了“先进先出”队列，通过这个队列来存储第一次发现的节点，以便下一次的处理；而对于再次发现的节点，我们不予理会——不放入队列，因为再次发现的节点：

1. 无非是已经处理完的了；

2. 或者是存储在队列中尚未处理的。

《算法导轮》对两种搜索都采用了很聪明的做法，用白色WHITE来标志未发现的节点，用灰色GRAY来标志第一次被发现的节点，用黑色BLACK来标志第二次被发现的节点。

于是有了：

BFS(G,s)
	for each vertex v in V[G]
		status[v] = WHITE
		/******其他初始化******/
	status[s] = GRAY	//s是原点
	queue q
	入队(q,s);
	while q非空
		t = 出队(q);
		for each vertex v in Adj[t]	//与t邻接的点
			if status[v] = WHITE	//只对未访问的操作
				status[v] = GRAY	//标记为第一次访问
				/******其他操作******/
				入队(q,v)
		status[t] = BLACK	//此点已经处理完了

导轮还在上面伪代码的“其他”中加入了访问长度和父节点的操作。此举可以算出，从源点到其他顶点路径的最少步数和它的具体路径。

关于广度优先搜索的一个简单应用：

假如有问题，每个村庄之间都通过桥来联通，先给出村庄的图，问村庄A到村庄B最少要通过多少座桥？这个问题可以很容易的转化为上面的BFS问题。

深度优先搜索

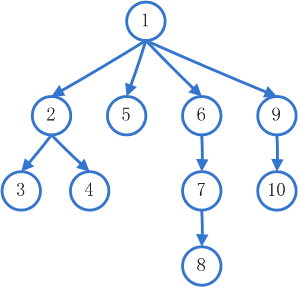
深度优先搜索（DFS），可以被形象的描述为“打破沙锅问到底”，具体一点就是访问一个顶点之后，我继而访问它的下一个邻接的顶点，如此往复，直到当前顶点一被访问或者它不存在邻接的顶点。

同样，算法导论采用了“聪明的做法”，用三种颜色来标记三种状态。但这三种状态不同于广度优先搜索：

1. WHITE 未访问顶点

2. GRAY 一条深度搜索路径上的顶点，即被发现时

3. BLACK 此顶点的邻接顶点被全部访问完之后——结束访问次顶点

DFS(G,s)
	for each vertex v in V(G)
		status[v] = WHITE
		/******其他初始化******/
	for each vertex v in V(G)
		if(status[v]==WHITE)
			DFS-VISIT(v)

DFS-VISIT(v)
	status[v] = GRAY
	for each vertex t in Adj(v)
		if status[t] = WHITE
			DFS-VISIT(t)
			/******其他操作******/
	status[v] = BLACK

通过给DFS搜索过程中给每一个顶点加时间戳，就可以实现拓扑排序了。实现拓扑排序需要：

对于每一个顶点，都有两个时间戳，分别这样来定义：

1. 在一顶点刚被发现的时候，标记此顶点的第一个时间戳；

2. 在结束此顶点的访问的时候，标记此顶点的第二个时间戳。时间戳可以用简单的123456来标记，只要能区分大小就行。

因此，你会发现，越早发现的点，他的第一个时间戳会越小，但是他的第二个时间戳会越大。

总结

两个算法都是O(V+E)，在用到的时候适当选取。在使用白灰黑标志的时候，突然明白了如何用深度优先搜索来判断有向图中是否存在环。

本文完 2012-05-16

Dylan http://daoluan.github.io/blog