【图论】有向图是否存在环

深度优先搜索可以用来实现“对有向图图中环的存在与否检测”，无向图环与否也差不多这样，但是这里主要是有向图。

在【图论】广度优先搜索和深度优先搜索中，“《算法导轮》对两种搜索都采用了很聪明的做法”，两种算法都标记了颜色。在深度优先搜索算法中，

  1. WHITE 未访问顶点

  2. GRAY 一条深度搜索路径上的顶点，即被发现时

  3. BLACK 此顶点的邻接顶点被全部访问完之后——结束访问次顶点

有向图的搜索过程

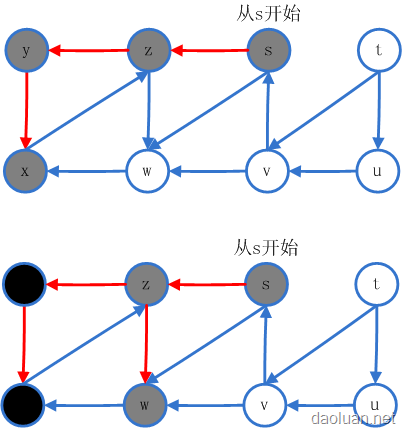
一个图的深度优先搜索过程：

在未探索完的一条深度优先搜索路径上，这条路径上的所有点都是灰色的（如果这些点被访问）；而搜索过程又不是并行的，所以程序每次只处在一条深度优先搜索路径的处理上。不知道理解没有，来看看图：

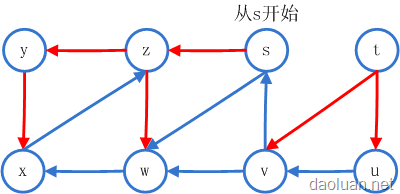
image.png

更形象点，介绍一下“DFS树”，在DFS过程当中，把真正走过的边加入DFS树当中，那些未真正走过的边不加入到DFS树当中，比如，从u到已经被访问的v，那么(u,v)就是一条未真正走过的边。来看图：红色边和其所连接的点组成了DFS树，在图中，DFS树会有两棵。

image.png

如果这样来定义DFS树的话，那么在这课DFS树当中只有树边了。

树边和反向边定义

树边的定义：如果顶点v在探寻边(u,v)边时候被首次发现的，那么(u,v)就是树边。

再来一个反向边的定义：

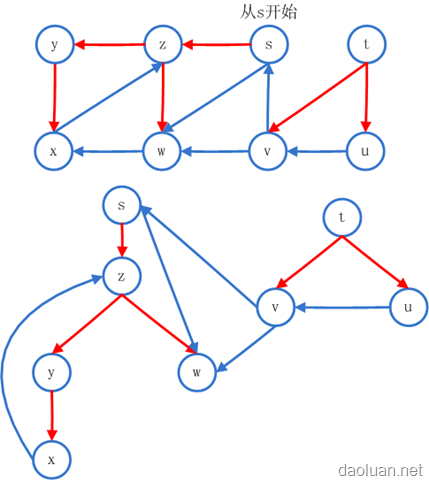
反向边：在DFS树中，连接顶点u到它某一祖先顶点v的边，也就是连接到那DFS条路径上点的边。

image.png

上面的两个图是等价的。

所以如果这么定义深度优先搜索树，对于下面的图它不可能存在反向边了，只有树边。把DFS树稍作修改，就可以得到原图（加上反向边，正向边，交叉边，《导论》有概念），

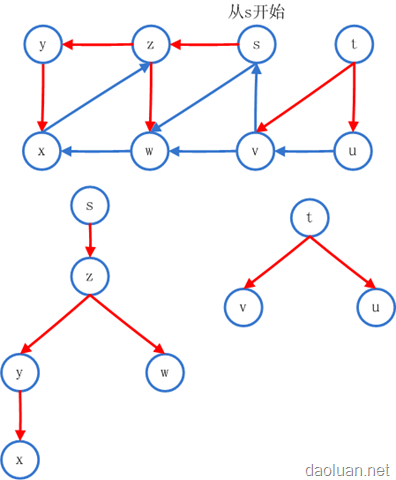
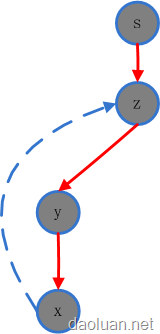
image.png

对于有向图，判断有无环就是判断它的“DFS树是否存在反向边”？那么如何判断呢？利用“颜色标记”法，就可以很简单做到。

image.png

上面的虚线边就表示当前DFS路径上探索到了一条反向边因为x和z点都是灰色的。当然对于有向图中是否存在环，并不影响DFS的最终效果——遍历。

于是有伪代码：

DFS(G,s)
    for each vertex v in V(G)
        status[v] = WHITE
        /******其他初始化******/
    for each vertex v in V(G)
        if(status[v]==WHITE)
            if !DFS-VISIT(v) = false
				return false

DFS-VISIT(v)
    status[v] = GRAY
    for each vertex t in Adj(v)
        if status[t] = WHITE
            DFS-VISIT(t)
		else if status[t] = GRAY
			return false
            /******其他操作******/
    status[v] = BLACK

所以核心就是判断反向边的问题。

本文完 2012-05-19

Dylan http://daoluan.github.io/blog

19 May 2012 会持续更新