• 写在最前面
• 正文
• 最为朴素的算法
• 一种改进的匹配

写在最前面

下面所涉及的字符串匹配算法是比较简答的，其中朴素算法在机器上测试，结果是随机数据即使是上百万，也可以秒杀，但是理论上来说Rabin-Karp算法会比朴素算法更优。

正文

字符串匹配问题：假定文本是一个长度为n的字符数组T[1…n]，模式是一个长度为m<=n的字符数组P[1…m]（即待匹配字符串），为的就是找到T中是否出现与P完全匹配的字串。

最为朴素的算法

穷举法可以说最为朴素的算法，他没有任何的优化，对T中所有长度为m的字串进行检测是否与P匹配。伪代码：

plain(P,T)
    m = strlen(P)
    n = strlen(T)
    for i=[0,n-m)
        if T[i...i+m-1]=P[0...m-1]
            打印“存在，匹配成功”

朴素算法时间复杂度为O[m*(n-m+1)]。

一种改进的匹配

前车之鉴，朴素算法每次都对T中长度为m的字串进行逐个字符的检测，一个更好的做法就是对T中长度为m的字串进行整体的匹配。假定所说的字符都是ASCII码，做法是这样的：

定义ASCII(P)为字符串P的ASCII码总和，把ASCII(P)模q（q任意，只要合理即可），得到一个值p，把通过这样计算得到的值记为ASCIIMOD(P)。这样整体匹配成为可能：

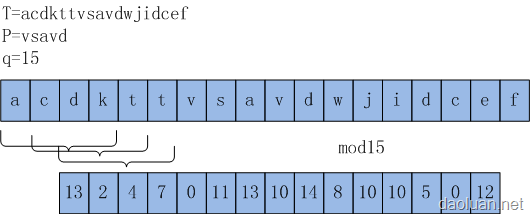
上图中，文本T=acdkttvsavdwjidcef，匹配内容P=vsav，设选模为q=15，ASCIIMOD(P)=13。所以在匹配的过程当中，只有mod15的值为13的字串才可以进行下一步的匹配。比如对于上图中的T中的前四个字符ACSIIMOD(“acdk”)=ASCIIMOD(P)=13，因此可以进行下一步的匹配。“下一步匹配”的原因是对于相同长度的不同字串A和B来说，可能存在ASCIIMOD(A)=ASCIIMOD(B)的现象。

这种方法虽然不能完全避免朴素中的“逐个字符匹配”，但如果适当选择模q，就可以大大减小“逐个匹配”的次数，从而提升性能。伪代码：

newcmp(P,T,q)
    //    预处理过程
    m = strlen(P)
    n = strlen(T)
    Q[0,n-m-1]
    p = ASCII(P) mod q    //    匹配内容P模q值
    sum = T[0]+T[1]+T[2]+T[3]
    Q[0] = sum mod q
    for i=[0,n-m)
        sum-=T[i]
        sum+=T[i+m]
        Q[i] = sum mod q

    //    匹配过程
    for i=[0,n-m)
        if Q[i]=p
            if T[i..i+m-1]=P[0..m-1]
                打印“存在，匹配成功”

上面的思路有个名字——Rabin-Karp算法，其预处理过程的计算方法很有意思（就是预处理里面的那个循环，据说是“霍纳法则”）。其复杂度为预计算里面的O(n+m)加上匹配过程中的O[(n-m-1)m]，好像也没有什么改进。但是这样想，“如果适当选择模q，就可以大大减小‘逐个匹配’的次数，从而提升性能”，匹配过程就可以近似为O(n-m-1)。

本文完 2012-06-06

Dylan daoluan.github.io/blog