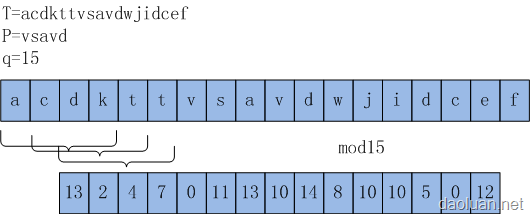
17周之后21周之前的大学生
期间千万大学学子,为了期末,拼了…士可杀,不可挂,即使头破血流,千疮百孔,也要杀出一条活路!各种综合实验,各种学习总结,各种复习,大学生们这个时候都是忙不过来。为了赶作业,熬到凌晨;为了复习,挑灯夜战。“今日事今日毕”,小学老师就教我们这么念;念了有十多年了,持之以恒者几许?
如果为了分数,这些奋斗意义不大。
有趣的字符串匹配“提示”
对于T=abacaababaack,P=abab
| a | b | a | c | a | a | b | a | b | a | a | c | k | |
| a | b | a | b | ||||||||||
| 匹配 | 1 | 2 | 3 | 0 |
如果此时有个提示,下一次匹配应从T字串的第三个字符开始匹配,因为从T的第二个字符开始匹配肯定是失败的。于是有:
| a | b | a | c | a | a | b | a | b | a | a | c | k | |
| a | b | ||||||||||||
| 匹配 | 1 | 0 |
又有提示,下一次从T的第四个字符开始匹配:
| a | b | a | c | a | a | b | a | b | a | a | c | k | |
| a | b | ||||||||||||
| 匹配 | 1 | 0 |
又有提示,下一次匹配,从T的第六个字符开始匹配:
| a | b | a | c | a | a | b | a | b | a | a | c | k | |
| a | b | a | b | ||||||||||
| 匹配 | 1 | 2 | 3 | 4 |
于是匹配成功。你将看到匹配自动机就是这么做的。
有限自动机进行字符串匹配
至于为什么叫“有限自动机”我也不知道,先这么叫着。
auto机就是一个协助匹配的状态表(或者图)。
算法开始的时候(在对T进行搜索之前),预先根据匹配内容P和字符集A构造出这个状态表,从而简化搜索过程。
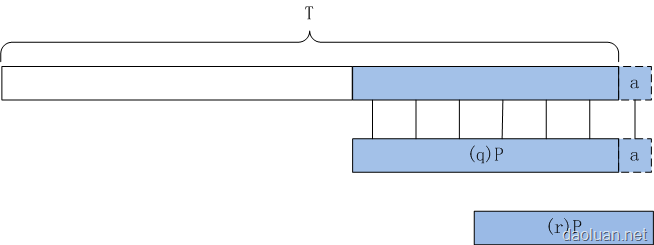
对于字串P,(k)P表示长度k的P的前缀;P(k)表示长度为k的P的后缀。比如P=abcdef,(3)P=abc,P(3)=def。
对于字串T,alpha(T)=max{k:T(k)==(k)P},可见这个涉及了两个字串,分别是文本T和匹配内容P。很恶心的公式,有例子,比如:P=abc,如果T=tab,那么alpha(T)=2;如果T=tabc,那么alpha(T)=3。
整一个算法的思想就是基于这么一个理论:如若alpha(T)=q(这个条件很重要),alpha(Ta)=alpha[(q)Pa]。这个搞定了,整个算法思想就通了。证明过程我只能用诸多“显然”的词汇来描述。 算法导论中有一个很经典的图:
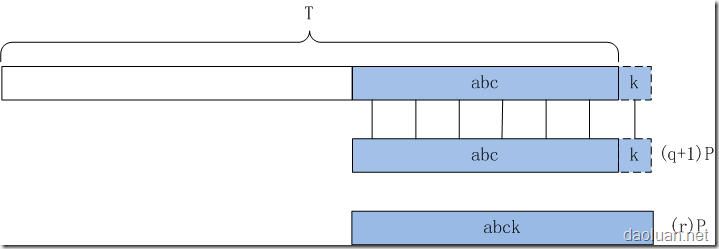
假定r=alpha(Ta),那么r<=q+1(条件alpha(T)=q),因为最理想的情况也就是r=q+1(图中的a字符刚好与P的第q+1字符匹配),此时也有r=q+1=alpha[(q)Pa]。
其他的情况一律满足r<q+1,又T(r)肯定是P的前缀,即T(r)=(r)P,所以r<=alpha[(q)Pa],即alpha(Ta)<=alpha[(q)Pa]。再来,因为(q)Pa肯定是T(q)a的后缀,alpha(Ta)>=alpha[(q)Pa]肯定成立。这样就证明了alpha(Ta)=alpha[(q)Pa]。
假定匹配字串P为和字符集为A,则计算出对于k=[1,m](m为P的长度),对于a∈A,计算出alpha[(k)Pa]。
一个具体的例子
看一个具体的例子: 假定,匹配内容P=acbaca,其字符集只涉及了{a,b,c},那么其对应的状态转换图:
补充说明红色线和绿色线。
红色:alpha(acbacb)=3,
| acbacb | a | c | b | a | c | b | X | X | X |
| P | X | X | X | a | c | b | a | c | a |
绿色:alpha(acbaa)=1,
| acbaa | a | c | b | a | a | X | X | X | X | X |
| P | X | X | X | X | a | c | b | a | c | a |
于是对于T=ktfacbacbacbkk,有了上面的状态转换图,匹配过程简单明了
| T | k | t | f | a | c | b | a | c | b | a | c | b | k | k |
| alpha | 0 | 0 | 0 | 1 | 2 | 3 | **4** | **5** | **3** | **4** | **5** | **6** | 0 | 0 |
加粗部分表示匹配成功。对于P=acbaca,T=ktfacb,把状态转换图变更会得到一个等价的表,这便于编程实现的:
| k | t | f | a | c | b | |
| 0 | 0 | 0 | 0 | **1** | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | **2** | 0 |
| 2 | 0 | 0 | 0 | 1 | 0 | **3** |
| 3 | 0 | 0 | 0 | **4** | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | **5** | 0 |
| 5 | 0 | 0 | 0 | **6** | 0 | 3 |
| 6 | 0 | 0 | 0 | 1 | 2 | 0 |
有限自动机进行字符串匹配的时间复杂度
如果在文本T中,除了与匹配内容P完全匹配的字符串,不存在任何的(k)P(即使没有这句话,下面的结论也是成立的),那么很明显能在O(n)内在文本T内完成对P的匹配。但是初始化过程比较费时间,需要O(n*m3)(n是字符集大小,m是匹配内容P的长度)。
一些问题
没怎么看懂这个算法?
你可以看看这篇文章所举的一个实例,看多几次,就会心领神会了。当然,结合算法导论来看是最好的。
代码呢,这么补贴代码?
如果真的需要的话,我可以日后补上。不过先看懂上面的理论,代码就可以很快打出来。Dylan日后补上。
本文可能未完 2012-06-10
Dylan daoluan.github.io/blog
10 June 2012 会持续更新