有向无回路图（Directed acyclic graph，DAG）的单源最短路径是基于这个理论：

倘若从点s到点v存在最短路径，即可达，所经过的点为：P0，P1，P2，P3….PN-1。
特别地，P0为s，v为PN-1。现对这个点序列按顺序进行松弛，即松弛顺序为（P0，P1），（P1，P2），（P2，P3）…，结果可以得到dist[v]=shortest_path(s,v)。注意，松弛顺序并非是严格先后，打比方：1，3，4在1，2，3，4中依旧是保持顺序的，但是可能中间会有“小插曲”。

又拓扑排序，可以知道，s到a肯定是不可达到，也就是不存在最短路径。故有期待已久的代码：

DAG(G)
	dist[n]    //    dist[i]表示s到i的最短路径
	TOPLLOGICAL-SORT(G)    //    拓扑排序
	for u∈拓扑排序后的有序点集
		for e(u,v)
		//    用e(u,v)松弛路径dist[v]

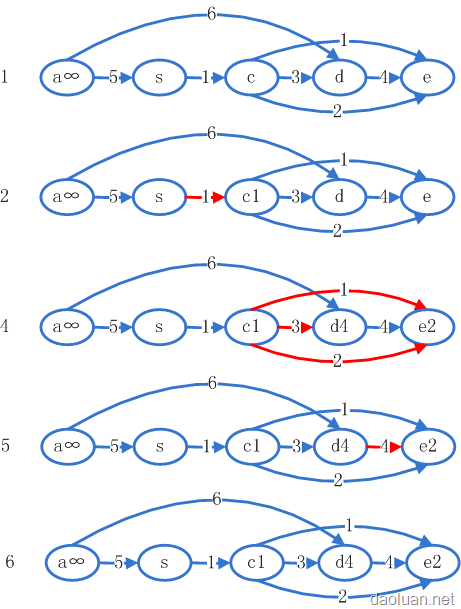
有图有证据：（红色表示当前在松弛的边）

此算法抠门有两个条件：1、有向 2、无环

本文完 2012-06-18

Dylan http://daoluan.github.io/blog/