• 最大堆和最小堆
• 上溯和下塑
• 堆的形成
• 堆排序
• max-heap实现priority_queue

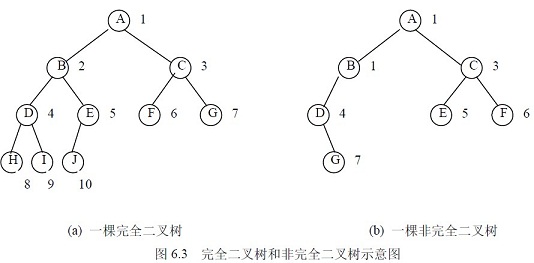
一句话的heap：一种数据结构，完全二叉树（若二叉树高h，除过最底层h层，其他层1~h-1都是满的；并且最底层从左到右不能有空隙。），但在实现上，它没有选择一般的二叉树数据结构（即一个节点包含指向两个孩子的指针），使用的是数组；heap最为常用的操作是上溯和下溯，它们在“维持堆”和“堆排序”中经常用到。这篇文章能让你快速回顾heap。

完全二叉树（左）和非完全二叉树（右）

完全二叉树的数组存储（对应上图左），X是实现上的技巧，刻意空出来

如果某节点位于数组i处，那么那么2i即为其左子结点，2i+1即为其右子结点。

最大堆和最小堆

堆有有最大堆和最小堆两种。最大堆即根节点的键值比其他所有节点键值都大；最小堆即根节点的键值比其他所有节点键值都小。只讨论最大堆，最小堆和最大堆思路如出一辙，便不一一复述了。

上溯和下塑

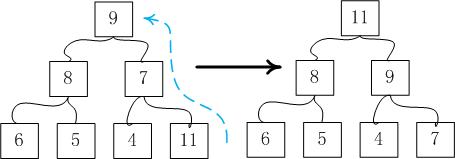
上溯操作主要用在“push_heap”过程中维持堆性质；下塑操作经常用在“sort_heap”过程中维持堆性质。

上溯：某节点与父节点比较，如果其键值比父节点大，即交换父子节点。重复上述操作，直到不需要交换或者到达根节点为止。

上溯

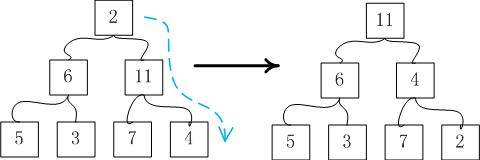
下塑：此节点为与堆顶，拿其与min（左子结点键值，右子结点键值）比较，如果父节点键值小过min，即交换父子节点。重复上述操作，直到不需要交换为止。

下溯

堆的形成

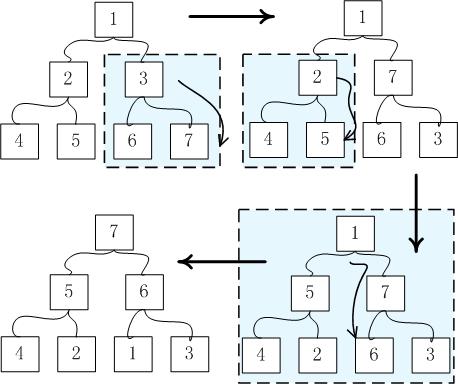
任务：给定一个数组，将其转换为最大heap。STL中make_heap()函数可以完成，它的思路：从最底层开始维持每一个子堆。看图：

make-heap

还有一种可行的思路，即：先假设堆中的元素个数为0，然后向（尾端+1）（意即尾端后的一个位置）push一个新的元素，然后在这个位置执行上溯操作。重复上述操作，直至数组内所有的元素都push完为止。我们发现这个方法也是可行的。

堆排序

任务：给定一个最大heap，实现数组排序。思路不拐弯抹角，很直接：因为堆顶对应最大的元素swap(堆顶节点，最大heap最右一个节点)；不处理最后一个节点，从堆顶下溯。注意，下溯操作过后，除过最后一个节点，现有数据仍为一个最大堆。

堆排序的算法复杂度可以达到O(NlnN)，在“排序算法家族”当中效率还是很靠前的。关于heap的算法都在STL中实现，STL只实现了最大堆。

......
vector<int> iv(a,a+7);
unsigned int i;

vector<int>::iterator beg = iv.begin(),
	end = iv.end(),ite;

for(ite = beg; ite!=end; ite++)
	cout << *ite << " ";
cout << endl;	/*1 3 9 11 21 100 4*/

make_heap(beg,end);

for(ite = beg; ite!=end; ite++)
	cout << *ite << " ";
cout << endl;	/*100 21 9 11 3 1 4*/

sort_heap(beg,end);

for(ite = beg; ite!=end; ite++)
	cout << *ite << " ";
cout << endl;	/*1 3 4 9 11 21 100*/
......

max-heap实现priority_queue

priority_queue带权值的queue，顺序入队之后，按照权值的大小出队。max-heap正好可以满足这个需求，max-heap的堆顶元素总是最大的。priority_queue在实现上已vector为底层容器，这与queue相差很大。

template<class _Ty,
	class _Container = vector<_Ty>,
	class _Pr = less<typename _Container::value_type> >
	class priority_queue
{......}

本文完 2012-10-19

Dylan http://daoluan.github.io/